| Función inversa |
| Definición (función inversa) Cita Dada una función $ f: A \to B $, llamaremos función inversa de $ f $, a la función $ f^{-1}: B \to A $ que verifica que $ f^{-1} \circ f = id_{A} $ y $ f \circ f^{-1} = id_{B} $. Teorema (existencia de la función inversa) Cita La función $f $ tiene inversa $ \Leftrightarrow f $ es una función biyectiva. Teorema (unicidad de la inversa) Cita Si la función $ f $ tiene inversa $ \Rightarrow $ ésta es única. Funciones reales de una variable Dada $ f:\mathbb{R}\to\mathbb{R} $, tenemos que $ f^{-1} $ es la inversa de $ f $ sii $ f(x)\circ f^{-1}(x) = f^{-1}\circ f(x) = x $. Por lo anterior tendremos que $ f^{-1} $ es una simetrización de $ f $ con respecto a $ y = x $, y viceversa. Ejemplo 1: Demostrar que la función $ f(x) = x + 2 $ posee inversa y hallarla. Notemos que $ f'(x) = 1 > 0 \Rightarrow f $ es estrictamente creciente y por ende biyectiva. Por el teorema de existencia de la inversa, existe $ f^{-1} (x) $. Ahora bien, para hallar la inversa, apliquemos el siguiente cambio de variable: $$ \left\{\begin{matrix} f(x) \rightarrow x \\ x \rightarrow f^{-1}(x) \end{matrix}\right. $$Efectuando operaciones:$$ f(x) = x + 2 \overset{C.V}{\Rightarrow} x = f^{-1}(x) + 2 \Rightarrow \boxed {f^{-1}(x) = x - 2} $$ A continuación se muestran $ f(x), f^{-1}(x) $ y su eje de simetría: 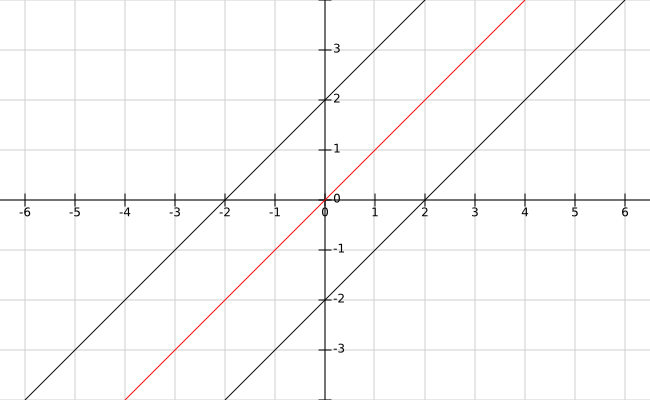 Ejemplo 2: Hallar la inversa de la función $ f:[0,+\infty) \to \mathbb{R} $ definida como $ f(x) = x^2-4 $. Notemos que $ f'(x)|_{[0,+\infty)} = 2·x|_{[0,+\infty)} \geq 0 \Rightarrow f $ es biyectiva $ \Rightarrow f $ tiene inversa. Comentario: notar que la función cuadrática no es biyectiva, razón por la cual nos tuvimos que restringir a un intervalo en el que sí lo es. En general, las funciones polinómicas siempre son sobreyectivas, pero sólo las impares son inyectivas. Para hallar la inversa de $ f $, efectuamos el cambio de variable: $$ \left\{\begin{matrix} f(x) \rightarrow x \\ x \rightarrow f^{-1}(x) \end{matrix}\right. $$Efectuando operaciones:$$f(x) = x^2 - 4 \overset{C.V}{\Rightarrow} x = (f^{-1}(x))^2 - 4\Rightarrow (f^{-1}(x))^2 = x + 4 \Rightarrow f^{-1}(x) = \pm \sqrt{x+4}$$De las dos opciones, tenemos que descartar la negativa (que corresponde a la otra mitad de la parábola). Entonces tendremos que $ f^{-1}(x) = \sqrt{x+4} $. A continuación se muestran $ f(x), f^{-1}(x)|_{[0,+\infty)} $ y su eje de simetría: 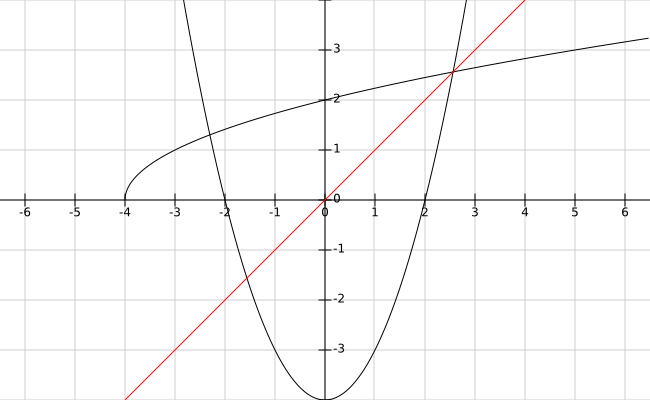 Ejemplo 3: Hallar la inversa de la función homográfica $ f:\mathbb{R} \setminus \left \{ 0 \right \} \to \mathbb{R}$ definida como $ f(x) = 1/(x+2) $. ----~---- Ahora intentemos hallar la inversa de la función $ f(x) = e^x + x $, la cual es una función biyectiva en $ \mathbb {R} $, y por el teorema de existencia de la inversa, sabemos que existe $ f^{-1}(x) $. Si razonamos de forma análoga a como lo hicimos en los casos anterior, llegaremos a una ecuación que no sabemos despejar; es más, no se puede despejar $ f^{-1}(x) $ en función de $ x $. Es decir, existe la inversa de $ f $ pero no se puede hallar una fórmula analítica explítica. Lo siguiente nos ayudará a estudiar la derivada de la inversa en un punto dado, que si bien entendemos que no es mucha información, resolverá bastantes dudas. Teorema (derivada de la función inversa) Cita Sea $ f $ una función derivable en $ I = (a,b) $ de forma tal que $ f'(x) > 0 $ en dicho intervalo. Entonces, $ f^{-1} $ es derivable en $ J = f(I) $ y verifica que: $$ (f^{-1})'(y) = \frac {1}{f'(f^{-1}(y))} $$ Demostración Como $ f'(x) > 0 $ entonces $ f $ es estrictamente creciente en $ I $. Luego, como $ f $ es derivable, es continua, y como además es monótona, su inversa también es continua (demostración que no veremos en detalle). Sea $ x = f^{-1}(y), x_{0} = f^{-1}(y_{0}) $: $$ \frac {f^{-1}(y) - f^{-1}(y_{0})}{y-y_{0}} = \frac {x-x_{0}}{f(x)-f(x_{0})} $$ Por la continuidad de $ f^{-1} $, cuando $ y \to y_{0} $ entonces $ x \to x_{0} $ y el segundo tiene límite $ 1/f'(x_{0}) $. Entonces: $$ (f^{-1})'(y_{0}) = \frac {1}{f'(x_{0})} = \frac {1}{f'(f^{-1}(y_{0}))} \quad \square $$ Ejemplo 4: Sea $ f:\mathbb{R} \to \mathbb{R} $ definida como $ f(x) = x^{17} + x^{13} + x^7 + x^3 + 5x-5 $. Hallar $ (f^{-1})'(4) $. Queremos hallar el valor $ n \in \mathbb {R} $ que verifica que $ f(n) =4 $ ya que $ f^{-1}(4) = n $. Así que $ f(n) = n^{17} + n^{13} + n^7 + n^3 + 5n-5 = 4 $ donde $ n = 1 $. Entonces: $$ (f^{-1})'(4) = \frac {1}{f'(f^{-1}(4))} = \frac {1}{f'(1)} = \frac {1}{45} $$ |