| Grafo euleriano |
| Definición: circuito euleriano Cita Sea $ G = (V,E) $ un grafo o multigrafo no dirigido sin vértices aislados. Entonces $ G $ admite un circuito euleriano si existe un circuito en $ G $ que recorre cada arista del grafo exactamente una vez. Teorema 1 Cita Sea $ G = (V,E) $ un grafo o multigrafo no dirigido sin vértices aislados. Entonces $ G $ admite un circuito euleriano si y sólo si: $ G $ es conexo y todo vértice de $ G $ tiene grado par. Ejemplo 1 Cita 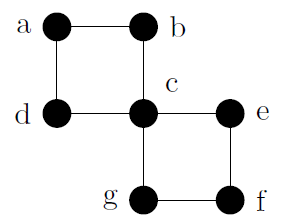 El anterior grafo sí admite ciclo euleriano, pues todos sus vértices son de grado par. Un posible ciclo euleriano es: $ d\rightarrow a\rightarrow b\rightarrow c\rightarrow g\rightarrow f\rightarrow e\rightarrow c\rightarrow d $. Notar que no es el único. Definición: recorrido euleriano Cita Sea $ G = (V,E) $ un grafo o multigrafo no dirigido sin vértices aislados. Entonces $ G $ admite un recorrido euleriano si existe un camino abierto de $ a $ a $ b $ en $ G $ que recorre cada arista de $ G $ exactamente una vez. Teorema 2 Cita Sea $ G = (V,E) $ un grafo o multigrafo no dirigido sin vértices aislados. Entonces $ G $ admite un recorrido euleriano si y sólo si: $ G $ es conexo y todo vértice de $ G $ tiene grado par, salvo exactamente dos. Ejemplo 2 Cita 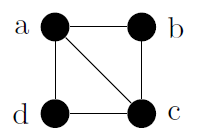 El anterior grafo no admite circuito euleriano, pues tiene dos vértices de grado impar. Sin embargo, por esta misma razón, sí admite recorrido euleriano. Un posible recorrido euleriano, es el siguiente: $ c\rightarrow b\rightarrow a\rightarrow d\rightarrow c\rightarrow a $. Notar que no es el único. Ejemplo 3 Cita 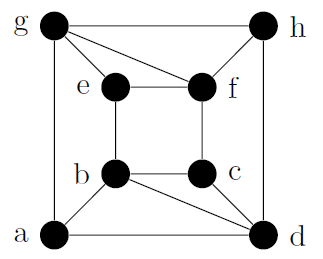 El anterior grafo no admite circuito euleriano ni recorrido euleriano, pues tiene cuatro vértices de grado impar. Dichos vértices son: $ \left \{ a,c,e,h \right \} $, todos de grado tres; mientras que los restantes son de grado cuatro. |