| Grafo hamiltoniano |
| Definición: ciclo hamiltoniano Cita Si $ G = (V,E) $ es un grafo o multigrafo con $ |V| \geq 3 $, decimos que $ G $ admite un ciclo hamiltoniano si existe en $ G $ un ciclo que contenga a cada vértice de $ V $. Observaciones Sea $ G = (V,E) $: 1. Si $ G $ tiene un ciclo hamiltoniano, entonces para $ v \in V, \mbox{grad} (v) \geq 2 $. 2. Si $ a \in V $ y $ \mbox {grad} (a) = 2 $, entonces las dos aristas incidentes con el vértice $ a $ deben aparecer en cualquier ciclo hamiltoniano de $ G $. 3. Si $ a \in V $ y $ \mbox {grad} (a) > 2 $, cuando tratamos de construir un ciclo hamiltoniano, una vez que hemos pasado por el vértice $ a $, dejamos de tener en cuenta las aristas no utilizadas incidentes en $ a $. 4. Al construir un ciclo hamiltoniano para $ G $, no podemos obtener un ciclo para un subgrafo de $ G $ a menos que contenga a todos los vértices de $ G $. Teorema 1 Cita Sea $ G = (V,E) $ un grafo no dirigdo sin lazos con $ |V| = n \geq 3 $. Si $ \mbox {grad} (x) + \mbox {grad} (y) \geq n, \forall x,y \in V $ no adyascentes, entonces $ G $ admite un ciclo hamiltoniano. Corolario 1 (Teorema de Dirac) Cita Sea $ G = (V,E) $ un grafo no dirigdo sin lazos con $ |V| = n \geq 3 $. Si $ \mbox {grad} (v) \geq n/2, \forall v \in V $, entonces $ G $ admite un ciclo hamiltoniano. Corolario 2 Cita Sea $ G = (V,E) $ un grafo dirigdo sin lazos con $ |V| = n \geq 3 $ y $ |E| \geq (n-1)(n-2)/2+2 $ entonces $ G $ admite un ciclo hamiltoniano. Ejemplo 1 Cita 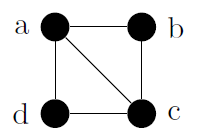 El anterior grafo admite ciclo hamiltoniano, una forma de ver esto es por el teorema de Dirac. Un posible ciclo hamiltoniano es: $ a \rightarrow b \rightarrow c \rightarrow d \rightarrow a $. Notar que no es el único. Ejemplo 2 Cita  Notemos que el anterior grafo no cumple la hipótesis del teorema de Dirac, sin embargo sí admite ciclo hamiltoniano. Un posible ciclo hamiltoniano es: $ a \rightarrow d \rightarrow c \rightarrow f \rightarrow h \rightarrow g \rightarrow e \rightarrow b \rightarrow a $. Notar que no es el único. Definición: camino hamiltoniano Cita Si $ G = (V,E) $ es un grafo o multigrafo con $ |V| \geq 3 $, decimos que $ G $ admite un ciclo hamiltoniano si existe en $ G $ un camino simple que contenga a cada vértice de $ V $. Teorema 2 Cita Sea $ G = (V,E) $ un grafo sin lazos, $ |V| = n \geq 2 $. Si $ \mbox {grad} (x) + \mbox {grad} (y) \geq n - 1, \forall x,y \in V $ con $ x \neq y $, entonces $ G $ admite un camino hamiltoniano. Corolario 3 Cita Sea $ G = (V,E) $ un grafo sin lazos con $ n \geq 2 $ vértices. Si $ \mbox {grad} (v) \geq (n-1)/2, \forall v \in V $, entonces $ G $ admite un camino hamiltoniano. Proposición 1 Cita Sea $ K_{n}^{*} $ un grafo dirigido completo; es decir $ K_{n}^{*} $ tiene $ n $ vértices y para cualquier par de vértices de $ x,y $ distintos exactamente $ (x,y) $ o $ (y,x) $ está en $ K_{n}^{*} $. Este grafo (llamado torneo) contiene siempre un camino hamiltoniano. |